Pytania i odpowiedzi
Fizyka Egzamin ARiSS 2023/2024
Zebrane pytania i odpowiedzi do zestawu.
Ilość pytań: 235
Rozwiązywany: 2097 razy
Pytanie 41
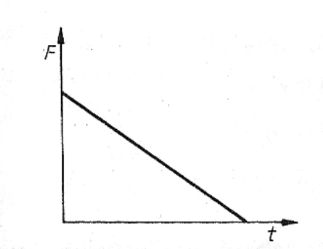
42. Na poruszające się po linii prostej ciało o masie m działa siła F, której zależność od czasu przedstawiono na rysunku. Możemy wnioskować, że w przedstawionej sytuacji ciało będzie się poruszało:
B. ruchem niejednostajnie przyspieszonym
Pytanie 42
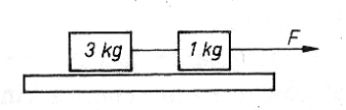
43. W sytuacji przedstawionej na rysunku (tarcie zaniedbujemy) siła napinająca nitkę ma wartość:
C. 3/4 * F
Pytanie 43
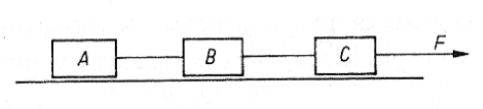
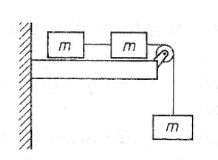
44. Trzy klocki o jednakowych masach m są połączone nieważkimi nitkami. Klocek C jest ciągnięty w prawo siłą F nadającą całemu układowi przyspieszenie. Jeżeli założymy, że nie ma tarcia między klockami i podłożem, to wypadkowa siła działająca na klocek B wynosi:
B. F/3
Pytanie 44
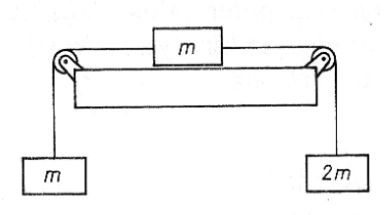
45. Jeżeli zaniedbamy tarcie i masę bloczków, to przyspieszenie ciężarków przedstawionych na rysunku wynosi około:
A. 2,45 m/s^2
Pytanie 45
Przyspieszenie ciężarków przedstawionych na rysunku (tarcie i masę bloczka zaniedbać) wynosi około:
A. 3,3 m/s^2
Pytanie 46
47. Z zasady zachowania energii mechanicznej wynika, że:
B. suma energii kinetycznej i potencjalnej układu jest stała, gdy w układzie działają tylko siły zachowawcze i siły zewnętrzne nie wykonują pracy nad układem
Pytanie 47
48. Jak zmienia się energia potencjalna spadającego swobodnie kamienia (w próżni)?
C. szybciej zmienia się przy końcu ruchu
Pytanie 48
49. Na ciało o masie m pozostające początkowo w spoczynku działa stała siła F. Jego energia kinetyczna po czasie t wynosi:
A. (F^2 * t^2) / 2m
Pytanie 49
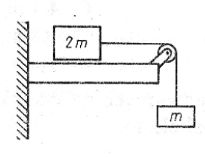
50. Jeżeli w sytuacji przedstawionej na rysunku (masę bloczka i tarcie zaniedbujemy) energia potencjalna ciężarka o masie m zmniejszy się o 30 J, to energia kinetyczna klocka o masie 2m powiększy się o wartość równą:
B. 20 J
Pytanie 50
51. Ciało o masie m wyrzucono pod kątem 60 stopni do poziomu, z prędkością v. Jeżeli zaniedbamy opór powietrza, to energia potencjalna ciała w najwyższym punkcie toru ma wartość:
D. 3mv^2/8
Pytanie 51
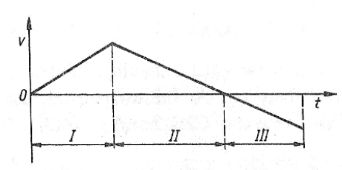
52. Ciało porusza się ruchem prostoliniowym. Na rysunku przedstawiono zależność prędkości v tego ciała od czasu t. Jaki znak (+,-) ma praca wykonana przez siłę wypadkową działającą na ciało w I, II, III przedziale czasu?
C. I (+), II (-), III (+)
Pytanie 52
53. Z powierzchni ziemi wyrzucono pionowo w górę ciało z prędkością v = 10 m/s. Na wysokości h = 3m, energia potencjalna tego ciała wynosiła E = 15J. Ile wynosiła na tej wysokości jego energia kinetyczna? (Przyjąć g = 10 m/s^2)
B. 10 J
Pytanie 53
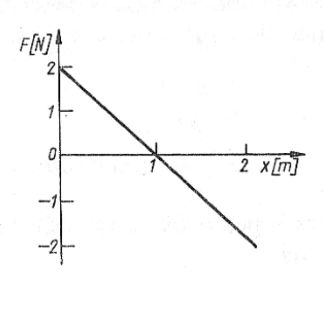
54. Pod działaniem siły F ciało porusza się po osi x. Na rysunku przedstawiono wykres zależności wartości siły F od położenia ciała. Na podstawie wykresu możemy wywnioskować, że praca wykonana przez tę siłę na drodze 2 m wynosi:
A. 0 J
Pytanie 54
55. Zakładamy, że siła potrzebna do holowania barki jest wprost proporcjonalna do prędkości. Jeżeli do holowania barki z prędkością 4 km/h jest potrzebna moc 4 kW, to moc potrzebna do holowania barki z prędkością 12 km/h wynosi:
C. 36 kW
Pytanie 55
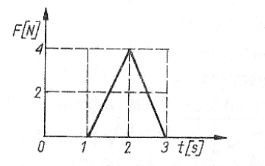
56. Na wykresie przedstawiono zależność od czasu siły działającej na ciało o masie 5 kg poruszające się po linii prostej. W rezultacie zmiana prędkości tego ciała wyniosła:
A. 0,8 m/s
Pytanie 56
57. Rozciągając pewną taśmę kauczukową o x stwierdzono, że siła sprężystości ma wartość F = ax^2 + bx, (a i b są stałymi). Minimalna praca potrzebna do rozciągnięcia tej taśmy od x = 0 do x = d wynosi:
D.

Pytanie 57
58. Wypadkowa siła działająca na cząstkę jest dana równaniem F = F0 * e^-kx (gdzie k > 0). Jeżeli cząstka ma prędkość równą zeru dla x = 0, to maksymalna energia kinetyczna którą cząstka osiągnie poruszając się wzdłuż osi x wynosi:
A. F0 / k
Pytanie 58
59. Czy układ zachowa swój pęd (całkowity), jeśli będzie nań działać stała siła zewnętrzna?
C. układ ten nie zachowa swojego pędu
Pytanie 59
60. Z działa o masie 1 tony wystrzelono pocisk o masie 1 kg. Energia kinetyczna odrzutu działa w chwili, gdy pocisk opuszcza lufę z prędkością 400 m/s wynosi:
A. 80 J
Pytanie 60
61. Z działa o masie 1 tony wystrzelono pocisk o masie 1 kg. Co można powiedzieć o energiach kinetycznych pocisku i działa w chwili, gdy pocisk opuszcza lufę?
B. prędkości działa i pocisku w chwili wystrzału są odwrotnie proporcjonalne do ich mas, więc energia kinetyczna pocisku będzie większa, niż energia kinetyczna działa


