Pytania i odpowiedzi
Fizyka Egzamin ARiSS 2023/2024
Zebrane pytania i odpowiedzi do zestawu.
Ilość pytań: 235
Rozwiązywany: 2099 razy
Pytanie 61
62. Kula o masie m uderza nieruchomą kulę o masie M i pozostaje w niej. Jaka część energii kinetycznej kuli zmieni się w energię wewnętrzną(zakładamy zderzenie idealnie sprężyste)?
D. M / (M + m)
Pytanie 62
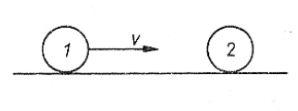
63. Jak wskazuje rysunek, kula bilardowa 1 uderza w centralnie identyczną, lecz spoczywającą kulę 2. Jeżeli uderzenie jest doskonale sprężyste, to:
A. kula 1 zatrzyma się, a kula 2 zacznie poruszać się z prędkością v
Pytanie 63
64. W trakcie centralnego (czołowego) zderzenia dwóch doskonale niesprężystych kul, energia kinetyczna zmienia się całkowicie w ich energię wewnętrzną jeśli mają:
C. równe i przeciwnie zwrócone pędy, a dowolne energie kinetyczne
Pytanie 64
65. W zderzeniu niesprężystym układu ciał jest:
A. zachowany pęd całkowity i zachowana energia całkowita układu
Pytanie 65
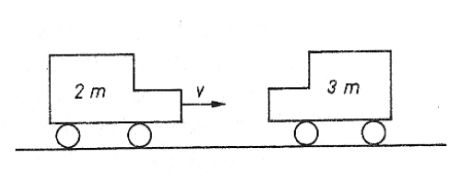
66. Wózek o masie 2m poruszający się z prędkością v zderza się ze spoczywającym wózkiem o masie 3m. Wózki te łączą się razem i poruszają się dalej z prędkością:
A. 2/5 * v
Pytanie 66
67. Człowiek o masie 50 kg biegnący z prędkością 5 m/s skoczył na wózek o masie 150 kg. Jaką prędkość będzie miał wózek z człowiekiem (tarcie pomijamy)?
A. 1,25 m/s
Pytanie 67
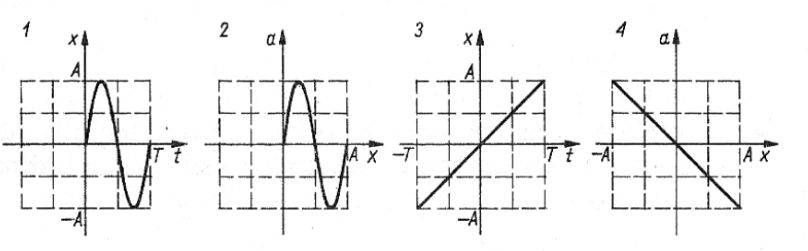
68. Które z wykresów dotyczą ruchu harmonicznego? (x - wychylenie, a - przyspieszenie, A - amplituda, t - czas)
D. tylko 1 i 4
Pytanie 68
69. Gdy moduł wychylenia punktu materialnego, poruszającego się ruchem harmonicznym, zmniejsza się, to:
A. moduł jego prędkości wzrasta, a moduł przyspieszenia maleje
Pytanie 69
70. W ruchu harmonicznym o równaniu x = 2cos0,4π * t okres drgań (czas t wyrażony w sekundach) wynosi:
C. 5 s
Pytanie 70
71. Maksymalne przyspieszenie punktu drgającego według równania x = 4sin(π/2 * t) (w którym amplitudę wyrażono w centymetrach, a czas w sekundach) wynosi:
A. π^2 cm/s^2
Pytanie 71
72. Amplituda drgań harmonicznych jest równa 5 cm, okres zaś 1 s. Maksymalna prędkość drgającego punktu wynosi:
D. 0,314 m/s
Pytanie 72
73. Punkt materialny porusza się ruchem harmonicznym przy czym okres drgań wynosi 3,14 s, a amplituda 1m
C. 2 m/s
Pytanie 73
74. Które z niżej podanych wielkości charakteryzujących ruch harmoniczny osiągają równocześnie maksymalne wartości bezwzględne?
D. wychylenie z położenia równowagi, przyspieszenie i siła
Pytanie 74
75. Ciało porusza się ruchem harmonicznym. Przy wychyleniu równym połowie amplitudy energia kinetyczna ciała:
A. jest trzy razy większa od jej energii potencjalnej
Pytanie 75
76. Ciało o masie m porusza się ruchem harmonicznym opisanym równaniem x = A sin 2π/T * t. Energia całkowita (tj. suma energii kinetycznej i potencjalnej) tego ciała wynosi:
A. 2π^2 * m * A^2 / T^2
Pytanie 76
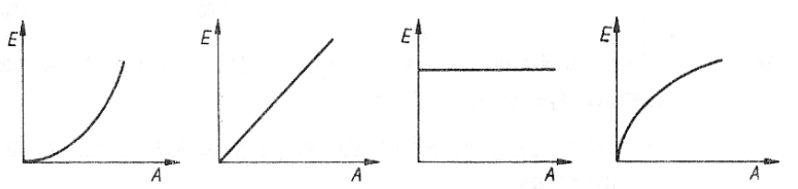
77. Na którym z wykresów przedstawiono zależność energii całkowitej E od amplitudy A dla oscylatora harmonicznego?
A.
Pytanie 77
78. Rozciągnięcie nieodkształconej początkowo sprężyny o pewną długość wymaga wykonania określonej pracy. Dodatkowe wydłużenie tej sprężyny (przy założeniu idealnej sprężystości) o tę samą długość wymaga wykonania:
C. trzy razy większej pracy
Pytanie 78
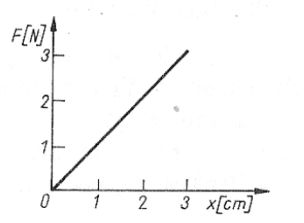
79. Na rysunku przedstawiono zależność F potrzebnej do ściśnięcia sprężyny, od odkształcenia sprężyny x. Praca wykonana przy ściśnięciu sprężyny o 3 cm wynosi:
B. 0,045 J
Pytanie 79
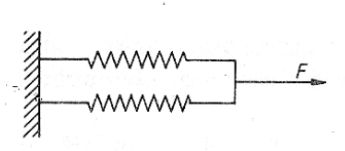
Pojedynczą sprężynę (lub układ sprężyn) rozciągamy w taki sposób, aby siła powodująca odkształcenie zawsze równoważyła siłę sprężystości. Przy wydłużeniu pojedynczej sprężyny o 12 cm jej siła sprężystości wynosi F.
80. Jeżeli dwie takie sprężyny połączymy, tak jak na rysunku, siłą zwiększająca się do F, to odkształcenie układu wynosi:
D. 6 cm
Pytanie 80
Pojedynczą sprężynę (lub układ sprężyn) rozciągamy w taki sposób, aby siła powodująca odkształcenie zawsze równoważyła siłę sprężystości. Przy wydłużeniu pojedynczej sprężyny o 12 cm jej siła sprężystości wynosi F.
81. Praca wykonana przy rozciąganiu takiego układu sprężyn siłą zwiększającą się do F jest:
B. dwa razy mniejsza niż w przypadku rozciągania jednej sprężyny



