Pytania: Fizyka Egzamin ARiSS 2023/2024 / Memorizer

Pytanie 1

1. Która z podanych jednostek NIE JEST jednostką podstawową układu SI?

B. niuton

SI to spójny układ siedmiu jednostek podstawowych: kilograma, metra, sekundy, ampera, kelwina, mola, kandeli.

Pytanie 2

2. Po dwóch równoległych torach kolejowych jadą w przeciwne strony dwa pociągi: jeden z prędkością 60 km/h, a drugi z prędkością 40 km/h. Prędkość pociągów względem siebie ma wartość:

D. 100 km/h zarówno przy zbliżaniu się, jak i przy oddalaniu

Pociągi jadą w przeciwne strony, co oznacza że ich prędkości mają przeciwne zwroty, a wypadkowa prędkość jednego względem drugiego jest sumą ich prędkości, czyli:

v = v1 + v2

Pytanie 3

3. Łódź płynie z miejscowości A do B i z powrotem. Prędkość łodzi względem wody wynosi 5 m/s, a prędkość wody względem brzegów wynosi 4 m/s. Średnia prędkość ruchu łodzi na trasie ABA miała wartość:

C. 1,8 m/s

v₁=v'+v" = 5m/s + 4m/s = 9m/s = prędkość motorówki wzgl. brzegu z prądem,

v₂=v'-v" = 5m/s - 4m/s = 1m/s = prędkość motorówki wzgl. brzegu pod prąd,

v = Δs/Δt........Δs=2s........Δt=t₁+t₂.....t₁=s/v₁........t₂=s/v₂

v = 2s/[t₁+t₂] = 2s/[s/v₁ + s/v₂] = 2s/[s(v₁+v₂)/v₁v₂] = 2s*v₁v₂/[s(v₁+v₂)]

v = 2v₁v2/[v₁+v₂] = [2*9m*1m/] /[10m/s] = 1,8m/s

Pytanie 4

4. Spadochroniarz opada na ziemię z prędkością v1 = 4 m/s bez wiatru. Z jaką prędkością v będzie poruszał się przy poziomym wietrze, którego prędkość v2 = 3 m/s?

A. 5 m/s

Obliczamy z pitagorasa, v1 to jest dłuższa przyprostokątna (pionowa), v2 jest krótszą przyprostokątną (poziomą), a v jest przeciwprostokątną:

v = sqrt(v1^2 + v2^2)

Pytanie 5

5. Pasażer pociągu poruszającego się z prędkością v = 10m/s widzi w ciągu czasu t = 3s wymijany pociąg o długości L = 75 m. Jaką wartość ma prędkość wymijanego pociągu?

C. 15 m/s

Pociąg nadjeżdżający z naprzeciwka o długości 75 m, był widziany przez pasażera przez 3s. To oznacza, że jego prędkość wynosiła 75m/3s. Jest to prędkość jednego pociągu względem drugiego, więc prędkość pierwszego pociągu i drugiego, więc należy je zsumować:

Vx + V = L/t

Vx + 10m/s = 75m/3s

Vx = 25m/s - 10m/s

Vx = 15 m/s

Pytanie 6

6. Jeżeli cząstka o masie m początkowo spoczywająca zaczęła się poruszać i jej prędkość dąży do prędkości światła w próżni c, to pęd cząstki:

C. rośnie do nieskończoności

Zgodnie z teorią względności Einsteina, pęd (p) cząstki o masie m gdy jej prędkość dąży do prędkości światła w próżni (c), można obliczyć za pomocą wzoru:

p = (m*v)/[sqrt(1 - (v/c)^2)]

p - pęd cząstki

v - prędkość cząstki

m - masa cząstki

c - prędkość światła w próżni

Jeśli prędkość cząstki (v) dąży do prędkości światła (c), względna prędkość v/c dąży do 1. Wówczas mianownik: sqrt(1-(v/c)^2) dąży do zera, co sprawia, że pęd dąży do nieskończoności.

Pytanie 7

7. Jeżeli energia kinetyczna poruszającej się cząstki jest dwa razy większa od jej energii spoczynkowej, to możemy wnioskować że jej prędkość w wynosi: (c - prędkość światła w próżni)

C.

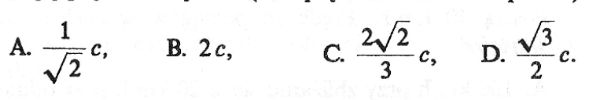
Pytanie 8

8. W akceleratorze dwie cząstki przybliżają się do siebie, poruszając się po tej samej linii prostej. Jeżeli każda z cząstek ma prędkość 0,8c względem ścian akceleratora, to jaka jest wartość ich prędkości względnej v?

D. 0,8c < v < c

Pytanie 9

9. Cząstka, której czas życia w jej układzie własnym wynosi 1s, porusza się względem obserwatora z prędkością v = 2c/3 (c - prędkość światła w próżni). Jaki czas życia t zmierzy obserwator dla cząstki?

B. t > 1s

Długość życia mierzona przez obserwatora (t) w teorii względności jest opisana przez równanie dylatacji czasu:

t = t0/sqrt(1-(v/c)^2)

t0 - czas życia w układzie własnym

v - to prędkość cząstki

c - to prędkość światła w próżni

t0 = 1s, v = 2c/3

Podstawiamy pod wzór i wychodzi nam:

t = 3/sqrt(5)

Wartość ta jest większa niż

1s, a więc odpowiedź B

Pytanie 10

10. Kolarz przebywa pierwsze 26 km w czasie 1h, a następne 42 km w czasie 3h. Średnia prędkość kolarza wynosiła:

B. 17 km/h

Pierwszy odcinek trasy s1 = 26km i w czasie 1h, drugi odcinek trasy s2 = 42km w czasie 3h. Sumujemy obie drogi i dzielimy przez sumę czasu

(s1+s2)/(t1+t2) = vśr

vśr = (26km+42km)/4h

vśr = 17km/h

Pytanie 11

Na podstawie przedstawionego wykresu można powiedzieć, że średnia prędkość w tym ruchu wynosi:

B. 5/4 m/s

Dzielimy to na odcinki czasowe, sumujemy prędkości i dzielimy przez ostatnią wartość t (bez sekund)

v1 = 1 m/s => t = 3s

v2 = 2 m/s => t = 1s

s1 = 3m

s2 = 2m

vśr = (s1+s2)/t

vśr = 5/4 m/s

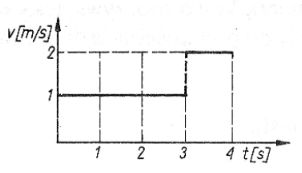
Pytanie 12

12. Zależność prędkości od czasu w pierwszej i drugiej minucie ruchu przedstawiono na poniższym wykresie. Prędkość średnia w czasie dwóch pierwszych minut ruchu wynosi:

B. 35 m/min

vśr1 = (v1 + v2)/2

vśr1 = 40/2

vśr1 = 20 m/min

vśr2 = (v1 + v2)/2

vśr2 = (40+60)/2

vśr2= 50 m/min

vśr = (vśr1 + vśr2)/2

vśr = (20+50)/2

vśr = 35 m/min

Pytanie 13

13. W pierwszej sekundzie ruchu ciało przebyło drogę 1m. W drugiej sekundzie 2m, a w trzeciej 3m. Jakim ruchem poruszało ciało w czasie tych trzech sekund?

D. zmiennym

t = 1s => s1 = 1m

t = 2s => s2 = s1 + 2m = 1 + 2 = 3m

t = 3s => s3 = s2 + 3m = 6m

Rysujesz wykres z ukośnymi kreskami do poszczególnych punktów, bazując na wykresie i treści zadania, przyjmujesz najbardziej ogólną odpowiedź, którą jest D

Pytanie 14

14. Ciało poruszające się po linii prostej ruchem jednostajnie przyspieszonym (v0 = 0) przebywa w pierwszej sekundzie ruchu 1m. Droga przebyta w drugiej sekundzie ruchu wynosi:

C. 3 m

S1 = 1m w czasie

t1 = 1s

s1 = v0 * t1 + (a * t1^2)/2

s1 = (a s^2)/2

a= 2m/s^2

s2 = v0 * t2 + (a * t2^2)/2

s2 = 4m

s = s2 - s1 = 4 - 1 = 3 m

Pytanie 15

15. Ciało porusza się ruchem jednostajnie przyspieszonym, w którym a = 2 m/s^2, v0 = 0. W której kolejnej sekundzie, licząc od rozpoczęcia ruchu, przebywa ono drogę 5m?

C. w trzeciej sekundzie ruchu

s = v0 * t + (a * t^2)/2

Pytanie 16

16. Zależność w prędkości od czasu przedstawiono na poniższym wykresie. W czasie trzech sekund ruchu ciało przebywa drogę:

D. 4,5 m

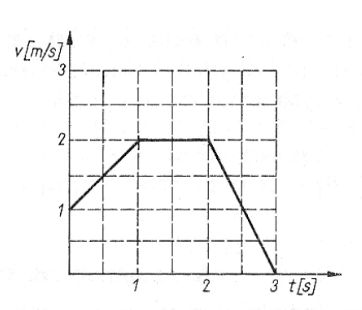
Liczysz pole znajdujące się pod wykresem

Pytanie 17

Z przedstawionego wykresu prędkości v jako funkcji czasu t wynika, że droga przebyta w czasie 3 sekund wynosi:

C. 3 m

Liczysz pole znajdujące się pod wykresem:

P = 1/2 * a * h

a = 3 s

h = 2 m/s

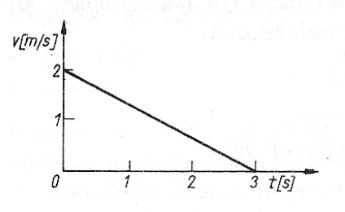
Pytanie 18

18. Ciało poruszające się ruchem jednostajnie przyspieszonym (v0 = 0) przebywa w drugiej kolejnej sekundzie od rozpoczęcia drogę 3 m. Przyspieszenie w tym ruchu wynosi:

B. 2 m/s^2

Stosujemy wzór:

s = (a * t^2)/2

sw2 = s2 - s1

3m = a/2 * (t2^2 - t1^2)

6m = 3a

a = 2m

Pytanie 19

19. Przyspieszenie pojazdu poruszającego się po prostej wynosi 1,2 m/s^2. Ile wynosiła średnia prędkość pojazdu w ciągu pierwszych trzech sekund? (v0 = 0)

B. 1,8 m/s

v = v0 + at

v = a * t = 3,6 m/s

vśr = (v0 + v)/2

vśr = 3,6/2 = 1,8 m/s

Pytanie 20

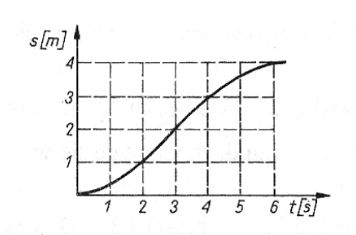
20. Punkt poruszał się po prostej w tym samym kierunku. Na rysunku przedstawiono zależność przebytej drogi s (w metrach) od czasu t (w sekundach). Posługując się tym wykresem, możemy wnioskować, że maksymalna prędkość w tym ruchu wynosiła około:

D. 1 m/s

Punktami obliczasz wszystkie prędkości i wybierasz największą (jeśli trzeba zaokrąglić, zaokrąglasz)

Pytania i odpowiedzi

Fizyka Egzamin ARiSS 2023/2024

Inne tryby